ELIPSE

Es el lugar geométrico de los puntos del plano cuya suma de distancias a dos puntos fijos es constante. Estos dos puntos fijos se llaman focos de la elipse.





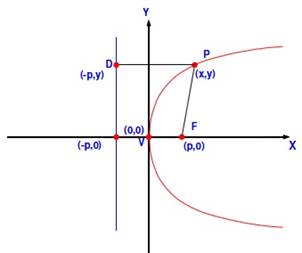
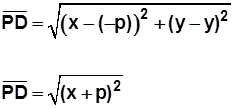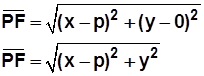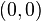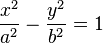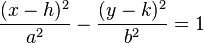para simplificar la explicación ubiquemos a los focos sobre el eje de las x, situados en los puntos F (c,0)  y F' (– c,0). Tomemos un punto cualquiera P de la elipse cuyas coordenadas son (x, y). En el caso de la elipse la suma de las distancias entre PF y PF' es igual al doble del radio sobre el eje x. Entonces: PF + PF' = 2a.   Aplicando Pitágoras tenemos que:

  

Elevamos al cuadrado ambos miembros para sacar las raíces y desarrollamos los cuadrados (ver operación) queda finalmente: 



Si la elipse estuviese centrada en un punto cualquiera (p, q) la ecuación debería de ser: 

Si desarrollamos los cuadrados obtendremos que: b2x2 + a2y2 – 2xpb2 – 2yqa2 + p2b2 + q2a2 – a2b2 = 0

Si hacemos:  A = b2
B = a2  
C = – 2pb2
D = – 2qa2
E = p2b2 + q2a2 – a2b2
tendremos la ecuación: Ax2 + By2 + Cx + Dy + E = 0, donde podemos comprobar que es igual que la de la circunferencia excepto que los términos A y B no tienen porqué ser iguales.

Ejemplo: Si tenemos la ecuación  4x2 + 9y2 + 24x – 8y + 81 = 0

Entonces tenemos que: A = 4 Þ 4 = b2 Þ b = 2;  B = 9 Þ 9 = a2 Þ a = 3

Los radios de la elipse son: sobre el eje x = a = 3; sobre el eje y = b = 2. Hallemos en centro (p, q).  

C = 24 Þ 24 = – 2pb2 Þ p = – 3 
D = – 54 Þ – 54 = – 2qa2 Þ q = 3
El centro es, entonces, (p, q) = (– 3, 3). Para verificar que se trate de una elipse calculemos E que debe tener el valor de 81. E = p2b2 + q2a2 – a2b2 = 81

La ecuación de la elipse queda: 



https://www.youtube.com/watch?v=849ryoz3LaU
https://www.youtube.com/watch?v=_d1SyjVGVpk

CIRCUNFERENCIA

Se denomina circunferencia al lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro. El radio de la circunferencia es la distancia de un punto cualquiera de dicha circunferencia al centro

si hacemos coincidir el centro con el origen de coordenadas, las coordenadas de cualquier punto de la circunferencia (x, y) determina un triángulo rectángulo, y por supuesto que responde al teorema de Pitágoras: r² = x² + y². Puesto que la distancia entre el centro (a, b) y uno cualquiera de los puntos (x, y) de la circunferencia es constante e igual al radio r tendremos que: r² = (x – a)² + (y – b)² Llamada canónica podemos desarrollarla resolviendo los cuadrados (trinomio cuadrado perfecto) y obtenemos

x² + y² – 2ax –2by – r² = 0.

Si reemplazamos   – 2a = D;     – 2b = E;     F = a² + b² – r² tendremos que:

x² + y² + Dx + Ey + F = 0

Ejemplo: Si tenemos la ecuación  x² + y² + 6x – 8y – 11 = 0

Entonces tenemos que: D = 6 Þ 6 = – 2a Þ a = – 3

 E = – 8 Þ – 8 = – 2b Þ b = 4

El centro de la circunferencia es (– 3, 4).  Hallemos el radio

 F = (– 3)² + 4² – r² Þ – 11 = (– 3)² + 4² – r² Þ r = 6

La ecuación de la circunferencia queda: (x + 3)² + (y – 4)² = 36

PARABOLA

En matemáticas, una parábola es la sección cónica resultante de cortar un cono recto con un plano cuyo ángulo de inclinación respecto al eje de revolución del cono sea igual al presentado por su generatriz. El plano resultará por lo tanto paralelo a dicha recta.Se define también como el lugar geométrico  de los puntos de un plano que equidistan de una recta llamada directriz y un punto exterior a ella llamado foco. En geometría proyectiva, la parábola se define como la curva envolvente de las rectas que unen pares de puntos homólogos en una proyectividad semejante o semejanza

La parábola aparece en muchas ramas de las ciencias aplicadas debido a que su forma se corresponde con las gráficas de las ecuaciones cuadráticas . Por ejemplo, son parábolas las trayectorias ideales de los cuerpos que se mueven bajo la influencia exclusiva de la gravedad 

Ecuaciones de la parábola con vértice en el origen

Primeramente, estudiaremos la ecuación de la parábola para los casos en que su vértice esté en el origen (coordenadas (0, 0) delPlano Cartesiano), y según esto, tenemos cuatro posibilidades de ecuación y cada una es característica.

Para iniciar nuestra explicación empezaremos con la parábola cuyo vértice está en el origen, su eje focal o de simetría coincide  con el eje de las X (abscisas) y que está orientada (se abre)  hacia la derecha.

Por definición, sabemos que, en una parábola  la distancia entre un punto “P” (no confundir con el “parámetro p”),   cualquiera de coordenadas (x, y), y el foco “F”  será igual a la distancia entre la directriz (D) y dicho punto, como vemos en la figura:

De lo anterior resulta:

                                        (trazo PD igual al trazo PF)

El trazo PD nace en el punto (x, y) y termina en el punto (–p, y) y podemos usar la fórmula para calcular distancia entre dos puntos:

                                                       
El trazo PF nace en el punto (x, y) y termina en el punto (p, 0), y también podemos usar la fórmula para calcular la distancia entre ellos:
                                                            

Sustituyendo en la expresión de distancias   resulta:

                                                          

Elevando ambos miembros de la ecuación al cuadrado y desarrollando, se tiene:

(x + p)² = (x – p)² + y²

x² + 2px + p² = x² – 2px + p² + y²

x² + 2px + p² – x² + 2px – p² = y²

Simplificando términos semejantes y reordenando la expresión, se obtiene:

y2 = 4px

que es ecuación de la parábola en su forma ordinaria o canónica.

Esta ecuación tiene leves variaciones según sea la orientación  de la parábola (hacia donde se abre).https://www.youtube.com/watch?v=N8WhvRJbGC8

HIPERBOLE

Una hipérbola es una sección cónica, una curva abierta de dos ramas obtenida cortando un cono recto por un plano oblicuo al eje de simetría, y con ángulo menor que el de la generatriz respecto del eje de revolución

Ecuaciones en coordenadas cartesianas: Ecuación de una hipérbola con centro en el origen de coordenadas  y ecuación de la hipérbola en su forma canónica: 

Ecuación de una hipérbola con centro en el punto 

Ejemplos:

a)

b)

Si el eje x es positivo, entonces la hipérbola es horizontal; si es al revés, es vertical. La excentricidad de una hipérbola siempre es mayor que uno.

https://www.youtube.com/watch?v=zMDjlUlArqI
https://youtu.be/6jP3VRiEa-o

SECCIONES CONICAS

Se denomina sección cónica (o simplemente cónica) a la curva intersección de un cono con un plano que no pasa por su vértice. Se clasifican en tres tipos: elipses, parábolas e hipérbolas.

En el gráfico siguiente se muestra dicha intersección: circulo,elipse,parábola,hipérbole

TIPOS:

En función de la relación existente entre el ángulo de conicidad (a) y la inclinación del plano respecto del eje del cono (ß), pueden obtenerse diferentes secciones cónicas, a saber:

¿ QUE ES LA MATEMATICA ?

 la matemática es una ciencia que, a partir de notaciones básicas exactas y a través del razonamiento lógico, estudia las propiedades y relaciones de los entes abstractos (números, figuras geométricas, símbolos). Mediante las matemáticas conocemos las cantidades, las estructuras, el espacio y los cambios. Los matemáticos buscan patrones, formulan nuevas conjeturas e intentan alcanzar la verdad matemática mediante rigurosas deducciones.

La matemática es considerada como la ciencia más compleja y elaborada, estudiada sólo por algunas selectas mentes. También se ha creído que se basa en abstracciones y que no da lugar a la experimentación. Sin embargo, un análisis menos superficial de la historia de la humanidad, deja claro que se trata de una construcción más. Las personas en su contacto con la realidad inmediata extraen resultados que posteriormente organizan en una ciencia más elaborada.

Definir matemática o matemáticas puede resultar complejo y acoger una única definición puede ser menos acertado que estudiar diversas definiciones.



Algunas definiciones de matemática se exponen a continuación:



· … es el arte de dar el mismo nombre a cosas distintas. Poincaré.

· …campo en el que no sabemos nunca de qué estamos hablando ni si lo que decimos es verdad. Bertrand Russell.

· …son la puerta y la llave de las ciencias. Francis Bacon

· la matemática actual es el estudio de las diversas estructuras y de las relaciones entre ellas. Bosh