
Ecuaciones en coordenadas cartesianas: Ecuación de una hipérbola con centro en el origen de coordenadas 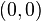 y ecuación de la hipérbola en su forma canónica:
y ecuación de la hipérbola en su forma canónica:
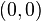 y ecuación de la hipérbola en su forma canónica:
y ecuación de la hipérbola en su forma canónica:
Ecuación de una hipérbola con centro en el punto 

Ejemplos:
a)
b)
Si el eje x es positivo, entonces la hipérbola es horizontal; si es al revés, es vertical. La excentricidad de una hipérbola siempre es mayor que uno.
https://www.youtube.com/watch?v=zMDjlUlArqI
https://youtu.be/6jP3VRiEa-o
https://youtu.be/6jP3VRiEa-o
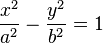
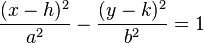


No hay comentarios:
Publicar un comentario