PARABOLA

En matemáticas, una parábola es la sección cónica resultante de cortar un cono recto con un plano cuyo ángulo de inclinación respecto al eje de revolución del cono sea igual al presentado por su generatriz. El plano resultará por lo tanto paralelo a dicha recta.Se define también como el lugar geométrico  de los puntos de un plano que equidistan de una recta llamada directriz y un punto exterior a ella llamado foco. En geometría proyectiva, la parábola se define como la curva envolvente de las rectas que unen pares de puntos homólogos en una proyectividad semejante o semejanza

La parábola aparece en muchas ramas de las ciencias aplicadas debido a que su forma se corresponde con las gráficas de las ecuaciones cuadráticas . Por ejemplo, son parábolas las trayectorias ideales de los cuerpos que se mueven bajo la influencia exclusiva de la gravedad 

Ecuaciones de la parábola con vértice en el origen

Primeramente, estudiaremos la ecuación de la parábola para los casos en que su vértice esté en el origen (coordenadas (0, 0) delPlano Cartesiano), y según esto, tenemos cuatro posibilidades de ecuación y cada una es característica.

Para iniciar nuestra explicación empezaremos con la parábola cuyo vértice está en el origen, su eje focal o de simetría coincide  con el eje de las X (abscisas) y que está orientada (se abre)  hacia la derecha.

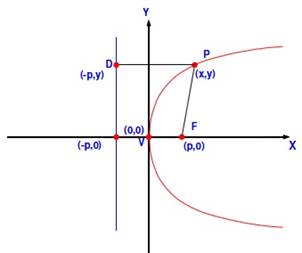
Por definición, sabemos que, en una parábola  la distancia entre un punto “P” (no confundir con el “parámetro p”),   cualquiera de coordenadas (x, y), y el foco “F”  será igual a la distancia entre la directriz (D) y dicho punto, como vemos en la figura:

De lo anterior resulta:

                                        (trazo PD igual al trazo PF)

El trazo PD nace en el punto (x, y) y termina en el punto (–p, y) y podemos usar la fórmula para calcular distancia entre dos puntos:

                                                       
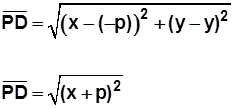
El trazo PF nace en el punto (x, y) y termina en el punto (p, 0), y también podemos usar la fórmula para calcular la distancia entre ellos:
                                                            

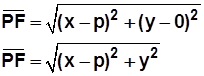
Sustituyendo en la expresión de distancias 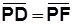  resulta:

                                                          

Elevando ambos miembros de la ecuación al cuadrado y desarrollando, se tiene:

(x + p)² = (x – p)² + y²

x² + 2px + p² = x² – 2px + p² + y²

x² + 2px + p² – x² + 2px – p² = y²

Simplificando términos semejantes y reordenando la expresión, se obtiene:

y2 = 4px

que es ecuación de la parábola en su forma ordinaria o canónica.

Esta ecuación tiene leves variaciones según sea la orientación  de la parábola (hacia donde se abre).https://www.youtube.com/watch?v=N8WhvRJbGC8